Linear Regression Calculator: Benefits for your Data Analysis

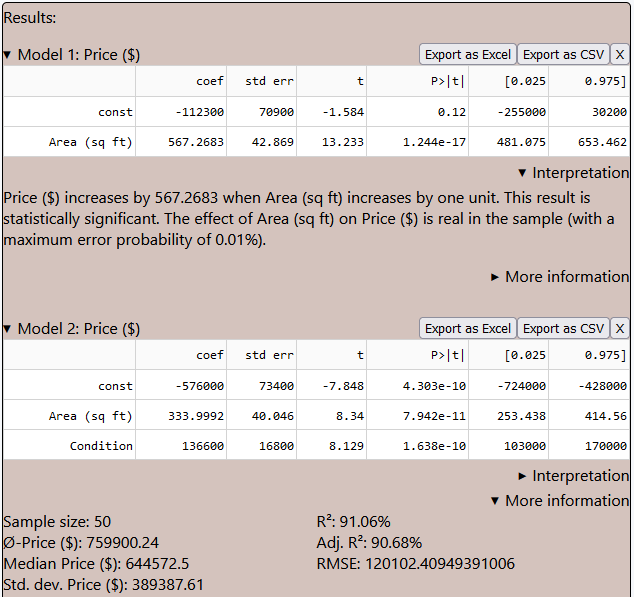
The interpretability of linear regression is a major advantage of this statistical method and contributes significantly to its widespread use in various scientific disciplines. A key feature of linear regression is its simplicity and transparency. The equation $\hat{y}={\hat{\beta }}_0+x\times {\hat{\beta }}_1$ provides a clear and understandable representation of the relationship between the dependent variable Y and the independent variable X. The intercept ${\hat{\beta }}_0$ indicates the value of Y when X is zero, while the slope ${\hat{\beta }}_1$ describes the change in Y when X increases by one unit. These parameters are directly interpretable and allow analysts to quantify the strength and direction of the relationship between the variables.

Moreover, linear regression allows the calculation of confidence intervals and p-values, which provide information on the statistical significance of the estimated parameters. These statistical measures help to assess the reliability of the results and to draw well-founded conclusions. Another advantage is the ability to use residual plots and other diagnostic tools to check the suitability of the model and potential violations of assumptions. Despite its simplicity, linear regression thus offers high explanatory and predictive power, making it an indispensable tool in data analysis.

Today, linear regression is used in many areas of data analysis and machine learning. By using regression models, researchers and analysts can identify patterns in large data sets and use them to predict future values. Linear regression models the relationship between a dependent variable and one or more independent variables by drawing a line through the data points that provides the best estimates of the dependent variable. This method is particularly useful for identifying linear relationships and trends in the data. One example is the analysis of sales data, where sales are examined in relation to advertising expenditure. Here, linear regression can help to understand the pattern of sales figures and predict future sales based on planned advertising measures.

Furthermore, linear regression enables the identification of outliers and unusual patterns that could indicate anomalies or special events. In practice, advanced techniques such as multivariate linear regression are often used to identify more complex patterns involving multiple independent variables.

The efficiency of linear regression is one of the main reasons for its widespread use in data analysis and machine learning. One of the greatest strengths of this method lies in its computational simplicity and comparatively low complexity. The calculation of the regression coefficients essentially requires the solution of a linear system of equations, which can be performed extremely quickly and resource-efficiently with modern computers, even with large data sets. This efficiency makes it possible to apply linear regression to a wide range of problems, from predicting share prices to analyzing market research data and evaluating scientific experiments.

Additionally, linear regression requires less memory and less computing time compared to more complex models, which makes it particularly useful for real-time applications. Another advantage is the robustness of the method against multicollinearity and the existence of good procedures for model evaluation, such as the coefficient of determination R² and the analysis of residuals. These properties make it possible to quickly and efficiently create valid models that provide reliable predictions. To summarize, linear regression is an extremely valuable method in modern data analysis due to its computational efficiency, simplicity and robustness.

Linear regression often serves as a foundation and basic model in the field of machine learning and deep learning. Despite the simplicity of this method, it provides a clear and understandable foundation on which more complex models can be built. Linear regression is often the first step in modelling as it illustrates basic concepts such as minimizing errors and optimizing parameters. These principles are essential for understanding and developing more advanced models. In machine learning processes, linear regression serves as a benchmark to evaluate the performance of new, more complex models. If a model based on linear regression delivers satisfactory results, you can be sure that it is a solid starting point for further analysis and model development.

Linear regression is also often used for feature selection and for interpreting the meaning of individual features, which is particularly important when working with high-dimensional data. In deep learning scenarios, linear regression can be used as a loss function or as an activation function in neural networks, especially in the regression of continuous values. Even though neural networks and other more complex models tend to be more powerful, understanding and applying linear regression is essential as it is a simple and interpretable model that provides insights into the data structure and relationships between variables. Thus, linear regression remains an indispensable tool and a starting point for the development and validation of more advanced machine learning models.

Companies can use linear regression to support their decision-making processes and thus make better business decisions. As a result, regression analytics offers significant benefits for companies looking to implement data-driven strategies. By applying this data analysis, companies can make accurate predictions and informed decisions based on historical data and trends. For example, sales figures can be analyzed in relation to advertising expenditure, pricing or seasonal influences in order to identify the most effective marketing strategies.

Linear regression enables the identification of key variables that have the greatest impact on business performance, facilitating targeted resource allocation and strategic planning. Another advantage is the ability to perform scenario analyses to simulate potential outcomes under different assumptions, thus minimizing risks and making better use of opportunities. By integrating linear regression into business analyses, companies can achieve greater accuracy in forecasting future developments, leading to improved competitiveness and long-term success.

Linear regression plays a crucial role in exploratory data analysis as it helps to uncover and understand patterns and relationships in the data. Exploratory data analysis is about initially identifying unknown structures and relationships within a dataset, and linear regression is a valuable tool for this. By creating a linear model, analysts can quantify the nature of the relationship between different variables by fitting a straight line to the data that best approximates the observed values. This makes it possible to identify both positive and negative correlations and assess whether and to what extent an independent variable influences a dependent variable.

The regression model also helps to identify outliers and unusual observations that may indicate special conditions or errors. In addition, by analyzing the regression coefficients and statistical significance, further insight can be gained into which variables actually have a significant impact on the result. These findings are particularly valuable for formulating hypotheses that can be tested in further analyses or experiments. Overall, linear regression in exploratory data analysis helps to gain a deeper understanding of the data, make well-founded assumptions and create the basis for further analytical steps and modeling.