Investigate Your Costs with Linear Regression

In today's competitive business landscape, making informed financial decisions is crucial for maintaining profitability and efficiency. Cost analysis plays a vital role in understanding expenses, optimizing budgets, and forecasting future financial needs. One of the most effective tools for gaining these insights is linear regression—a powerful method that helps businesses identify cost patterns, predict future spending, and make data-driven decisions. By leveraging historical data, companies can uncover relationships between costs and key business factors, allowing them to streamline operations, improve pricing strategies, and enhance overall financial planning. This article explores how businesses can apply linear regression to cost analysis, ensuring smarter financial management and strategic growth.

Knowing the value of linear regression in cost analysis is one thing, but seeing it in action is where its true impact becomes clear. Businesses across industries use this approach to uncover cost drivers, optimize spending, and make strategic financial decisions. Whether it's predicting manufacturing expenses, analyzing marketing ROI, or streamlining operational costs, linear regression provides actionable insights that drive efficiency and profitability. In the following section, we'll explore several practical use cases where businesses can apply linear regression to gain a clearer understanding of their costs and enhance decision-making.Understanding the value of linear regression in cost analysis is one thing, but seeing it in action is where its true impact becomes clear. Businesses across industries use this approach to uncover cost drivers, optimize spending, and make strategic financial decisions. Whether it's predicting manufacturing expenses, analyzing marketing ROI, or streamlining operational costs, linear regression provides actionable insights that drive efficiency and profitability. In the following section, we'll explore several practical use cases where businesses can apply linear regression to gain a clearer understanding of their costs and enhance decision-making.

Use case 1

Optimize Your Product Offering

For any business, balancing product availability with customer demand is key to maximizing revenue while minimizing waste. Consider this example in the fast-paced world of gastronomy: Imagine a coffee shop that sells a variety of pastries alongside its signature coffee drinks. How many croissants or cookies should it stock each day to meet demand without overspending on inventory or dealing with unsold leftovers? By analyzing past sales data, a business can identify patterns such as how pastry sales fluctuate based on the number of coffee drinks sold. With this insight, coffee shop owners can make data-driven stocking decisions, ensuring they always have the right amount of inventory to satisfy customers while keeping costs under control.

In this case, you might have data that looks like this:

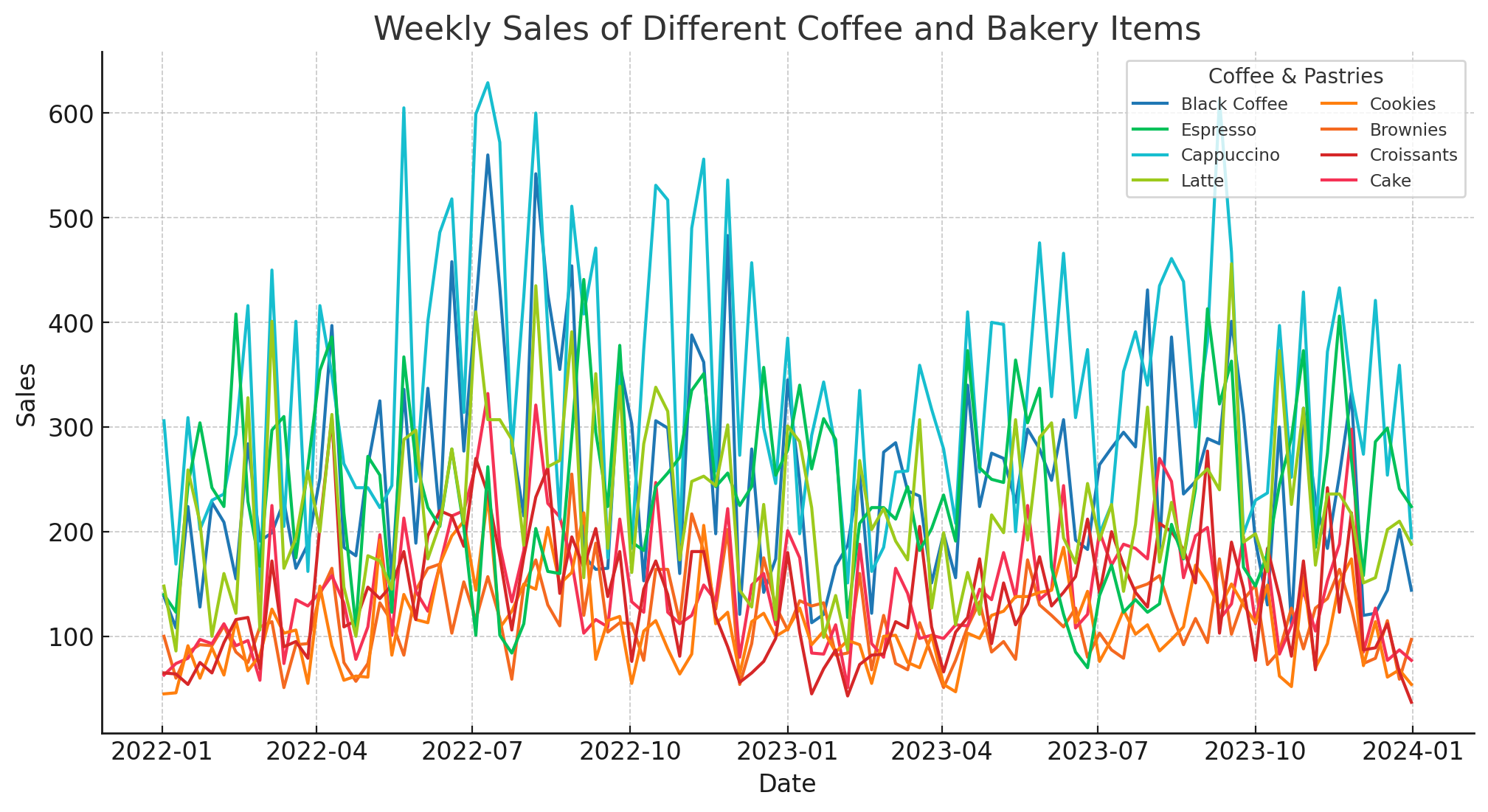
We can see peaks and valleys in sales, indicating seasonal influences and weekly demand variations. For example, sales tend to rise during peak holiday seasons or weekends. Factoring in these trends ensures the right balance of pastries is available during high-demand periods without overstocking during slower weeks. While all pastries exhibit a degree of correlation with coffee sales, certain items such as croissants and brownies show stronger alignment with coffee demand. This indicates they are preferred pairings, making them priority stock items. On the other hand, less popular items, like cookies, may require different stocking strategies. By leveraging historical data, coffee shop owners can use predictive modeling to optimize procurement. If past trends show that a 10% increase in cappuccino sales leads to a 7% increase in croissant demand, inventory adjustments can be made proactively. This approach prevents shortages that could impact sales while minimizing waste from unsold items.
For now, let's analyze aggregate demand and product data:

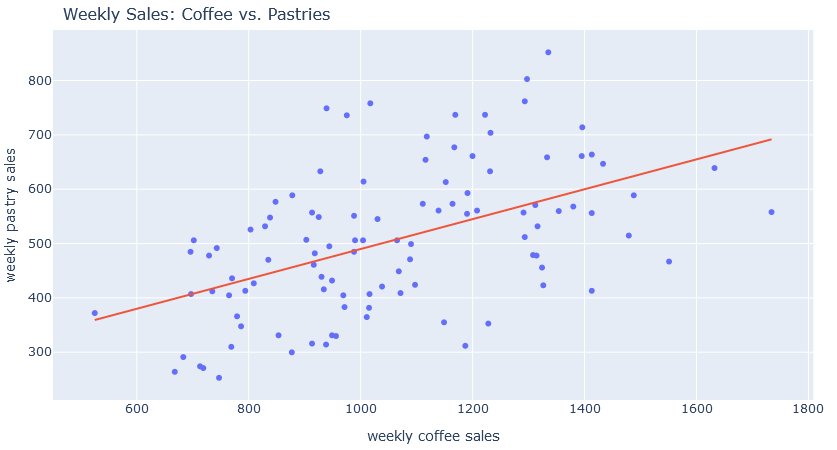
With linear regression, coffee shops (or any business in general) can use their past real sales data and make accurate inventory decisions. The orange trend line represents a linear regression model, which helps quantify the relationship between coffee and pastry sales. With this model, businesses can forecast the expected pastry sales given a certain number of coffee orders. For example, if a coffee shop anticipates selling 1,200 cups of coffee in a week, the model provides an estimate of how many pastries should be stocked to meet demand. By leveraging this predictive approach, coffee shop owners can strike the right balance in inventory management. Instead of relying on guesswork, they can use data-driven insights to prevent overstocking (which leads to waste) or understocking (which results in lost sales).
After running the analysis, our coffee shop might see results like these:

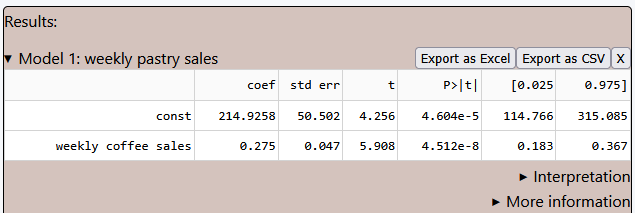
The key findings for the relationship between weekly coffee sales and weekly pastry sales are:

• const = 214.93:
  This represents the baseline number of pastry sales when coffee sales are zero. In practical terms, even if no coffee is sold, around 215 pastries would still be purchased, likely due to customers who buy pastries independently of coffee.
• weekly coffee sales = 0.275
  This indicates that for every additional cup of coffee sold, pastry sales increase by approximately 0.275 units. For example, if a coffee shop sells 1,000 more cups of coffee in a week, they can expect to sell around 275 more pastries!
  → The p-value for the coffee sales coefficient is 4.512e-8, which is very close to zero. This means the relationship is statistically significant, and there is strong evidence that coffee sales impact pastry demand.

By knowing these exact numbers, coffee shop owners have a data-driven foundation for inventory and sales decision-making. Linear regression improved stock management and reduced waste. Moreover, business owners can use these results as a basis for promotions or bundling strategies like combo deals.

Use case 2

Human Resources and Workforce Planning

Managing workforce costs effectively is crucial for maintaining profitability and growth. Human Resources and workforce planning involve complex decisions about hiring, salaries, benefits, and productivity, all of which impact the bottom line. Additionally, predicting employee turnover by analyzing factors like as job satisfaction, salary, work environment, and performance metrics is also crucial in order to develop strategies to retain talent. By leveraging data-driven insights, businesses can make informed decisions to optimize labor costs while ensuring they have the right talent in place. One powerful tool for achieving this is linear regression, which helps analyze historical workforce data to predict future costs and trends.
Consider this example: We want to optimize staffing levels for events that we organize. Staffing too little or too much can harm your business. Using historical data, you can apply linear regression to correlate event duration with staffing needs.
Image this kind of demo data:

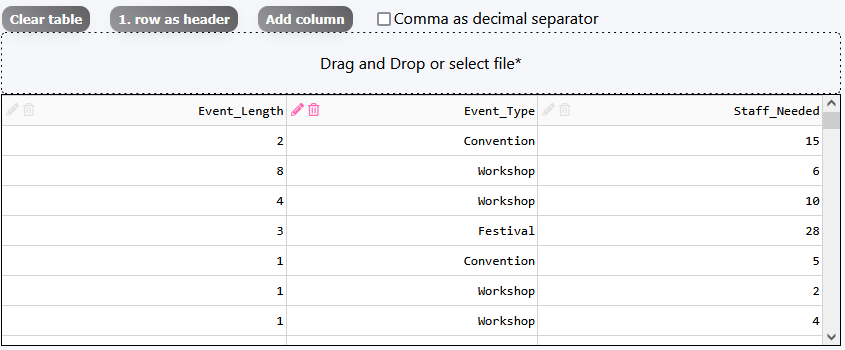
If data shows that some events consistently require 20% more staff, you can optimize your staffing schedule accordingly. You can also use regression analysis to understand the relationship between staff levels and event duration, ensuring that you have enough staff on hand for the busiest event types without overspending during shorter events. This targeted approach reduces labor costs and improves customer satsifaction by ensuring guests or clients are served well.

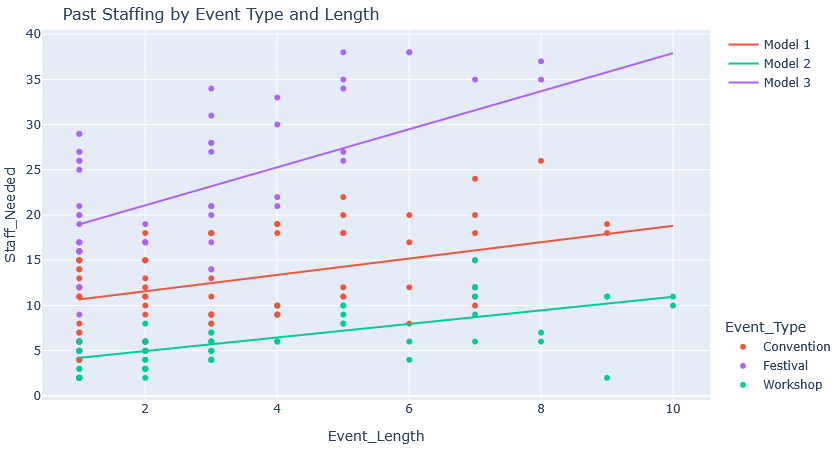
By analyzing historical staffing data, your business can better predict the number of employees needed for different types of events and optimize labor costs. The graph above illustrates past staffing levels based on event type and duration. Each event type—Convention, Festival, and Workshop—has a distinct staffing pattern, represented by different regression models. The trend lines highlight how workforce needs increase as event length extends. When running linear regression, we can first see the following:

• Conventions (Red - Model 1): These events show a moderate increase in staff needs as the event length grows. Businesses planning conventions can use this trend to estimate labor costs for future events based on duration.
• Festivals (Purple - Model 3): Festivals require significantly more staff than other event types, with a steep upward trend. This suggests that festivals have higher operational demands, likely due to crowd management and logistics.
• Workshops (Green - Model 2): Workshops have the lowest staffing needs and a relatively gradual increase over time. This indicates a more stable workforce requirement, allowing businesses to optimize labor costs efficiently.

But the numerical results from the linear regression analysis offer even more actionable insights:

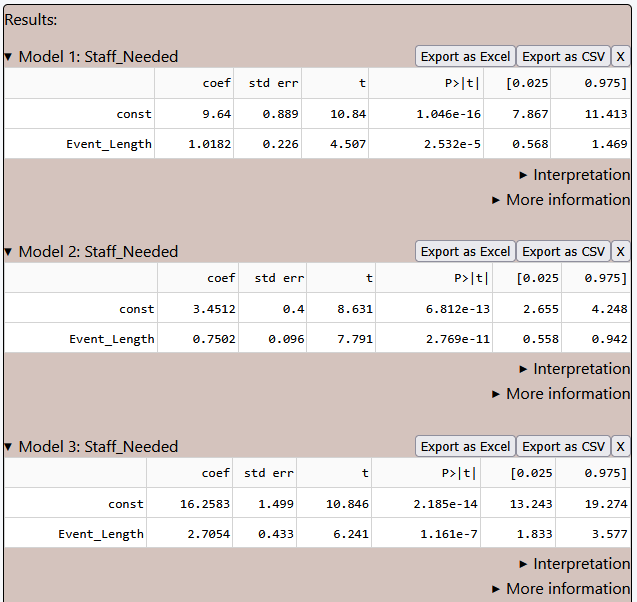
When looking at the coef column, we see that:

• Conventions have a moderate baseline staffing need and a gradual increase in staff requirements as event length increases. Businesses planning conventions can expect a linear but controlled growth in staffing costs based on event duration.
  → On average, a convention requires around 9 staff members, even if the event length is one day. For each additional event day, staffing needs increase by 1.02.
• Workshops require the least number of staff initially and show the slowest increase in staffing demand as event length grows. This suggests workshops are more cost-efficient in terms of labor, making them a favorable option for businesses with limited staffing budgets.
  → A workshop typically requires ca. 3 staff members even if the workshop lasts one day. For each additional day, staffing needs increase by 0.75.
• Festivals demand the highest initial workforce and show the steepest increase in staffing requirements as duration increases. This suggests that festivals incur the highest labor costs compared to conventions and workshops. Businesses must account for these costs when planning festival budgets and ensure they have sufficient staff to handle the crowd and logistics.
  → Festivals require a high initial workforce of about 16 staff members, even for one day festivals. Staffing needs increase significantly (2.71 per day) as festivals get longer.

Now what are the business implications?

1. Workforce Planning:
   • Workshops require the least staffing effort, making them cost-efficient.
   • Conventions have a steady but manageable increase in labor needs.
   • Festivals demand the most staff, both initially and as event duration extends.
2. Cost Optimization:
   • Businesses should allocate labor resources more aggressively for festivals.
   • Conventions allow for more controlled workforce growth.
   • Workshops can be run with minimal staffing, reducing labor costs
3. Budget Forecasting:
   • Using these models, companies can predict staffing costs based on event duration.
   • Forecasting labor expenses accurately enables better financial planning and decision-making.

Use case 3

Investigating Supply Chain and Logistics Costs

Managing supply chain and logistics costs is a constant challenge for businesses striving to improve efficiency and profitability. Factors such as fuel prices, shipment distances, transport modes, and cargo volume all influence transportation expenses, but understanding how they interact can be complex. By leveraging data-driven analysis, companies can uncover patterns and relationships that help them make smarter decisions. One effective approach is to examine these cost factors systematically, identifying opportunities to optimize shipping routes and transport modes, ultimately leading to reduced expenses and improved operational efficiency.
For example, consider this business use case analysis:

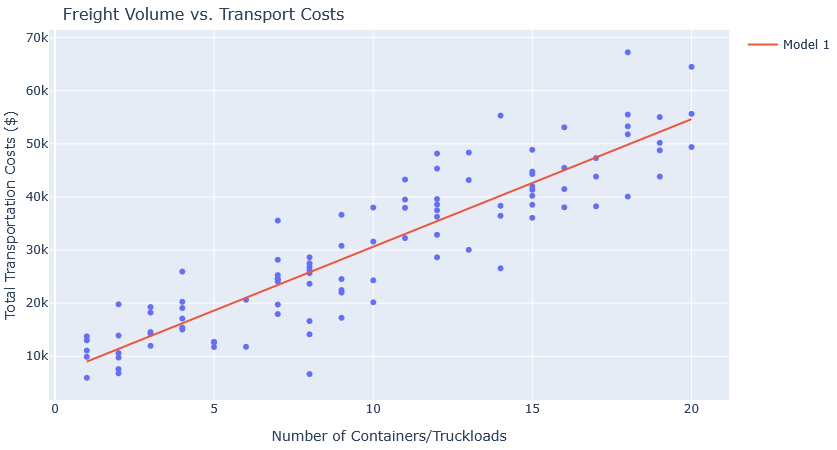
The scatter plot above illustrates the relationship between freight volume measured by the number of containers or truckloads—and total transportation costs. Each blue dot represents a recorded shipment, and the red line represents a trendline derived from a linear regression model. From the visualization, a clear upward trend can be observed, indicating that as the number of containers or truckloads increases, transportation costs also rise. However, the data also show some variation, suggesting that factors beyond freight volume like fuel prices, route efficiency, and transport mode can influence costs.
The linear trendline provides a simplified way to estimate transportation expenses based on shipment volume. Businesses can use this insight to forecast logistics costs and identify opportunities for optimization. For example, if a company notices a disproportionately high increase in costs beyond a certain shipment volume, it may explore bulk shipping discounts, alternative routes, or mode shifts (e.g., from trucking to rail or sea freight) to mitigate expenses. Additionally, the scatter pattern suggests that cost efficiency can vary even at similar shipment volumes. This variation could be due to inconsistent fuel pricing, peak-time demand surcharges, or underutilized cargo space. A deeper analysis incorporating these variables would allow companies to refine their cost estimation models further and implement more cost-effective logistics strategies:

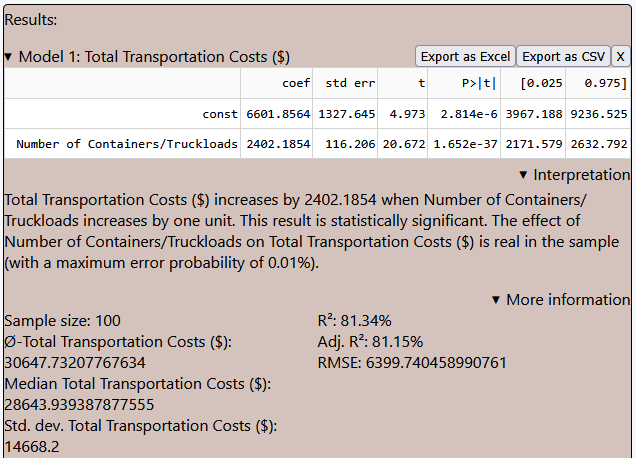
The regression analysis provides key insights into the relationship between the number of containers or truckloads and total transportation costs. Here is what the results indicate:

1. Impact of Freight Volume on Costs:
   • The coefficient for the Number of Containers/Truckloads is 2402.1854, meaning that for every additional container or truckload, total transportation costs increase by approximately $2,402.
   • This result is statistically significant (p-value: 1.652e-37), indicating strong evidence that shipment volume significantly affects transportation costs.
2. Fixed Costs and Baseline Expense
   • The constant term (intercept) is $6,601.86, suggesting that even if no shipments were made, there would still be a base level of transportation-related expenses (such as fixed overhead costs or fleet maintenance).
3. Model Performance and Reliabi
   • The R² value is 81.34%, meaning that 81.34% of the variation in transportation costs is explained by the number of containers/truckloads. This suggests a strong predictive capability.
   • The RMSE (Root Mean Square Error) is 6,399.74, indicating the typical deviation of actual transportation costs from the predicted values.

Business Implications:
Companies can use this model to predict transportation costs based on shipment volume, aiding in budgeting and financial planning. Since costs increase linearly with shipment volume, businesses may explore strategies such as consolidating shipments, using intermodal transport, or negotiating bulk rate discounts to reduce per-unit costs. While shipment volume explains a large portion of cost variations, the remaining 18.66% (1 - R²) suggests other factors, such as fuel costs, route optimization, and seasonal demand fluctuations, should be explored for further efficiency gains.
→ NOTE THAT regardless of your shipment volume and logistics, this model analyses is applicable to a wide range of businesses! Whether you have 10, 100, 1000 or 10,000 shipments per day, week or month or whether the shipments are made via parcel, trucking, rail or air freight: Linear regression is how you can make data-driven decisions to streamline your logistics operations, enhance cost efficiency, and improve overall supply chain performance.

Use case 4

Managing Your Inventory

Striking the right balance between inventory levels and ordering frequency is a challenge every retailer faces. Order too frequently, and transportation costs can skyrocket. Order too infrequently, and high storage costs eat into your margins. How do you determine the sweet spot? By analyzing past ordering patterns and costs, businesses can identify trends that reveal the most cost-effective approach. A data-driven strategy can help retailers minimize expenses while ensuring products are always available when customers need them. For instance, reasonable explanations for varying costs are:
→ 1. Large Inventory Stockpile
When companies order infrequently, they must store more inventory to meet demand between orders. This requires larger warehouses, increasing rent, utilities, and security costs. More inventory means higher storage fees, insurance costs, and maintenance.
→ 2. Higher Risk of Product Obsolescence
Slow-moving inventory risks becoming obsolete, outdated, or expired (especially for electronics, fashion, or perishables). Businesses may need to discount or dispose of unsold stock, increasing losses.

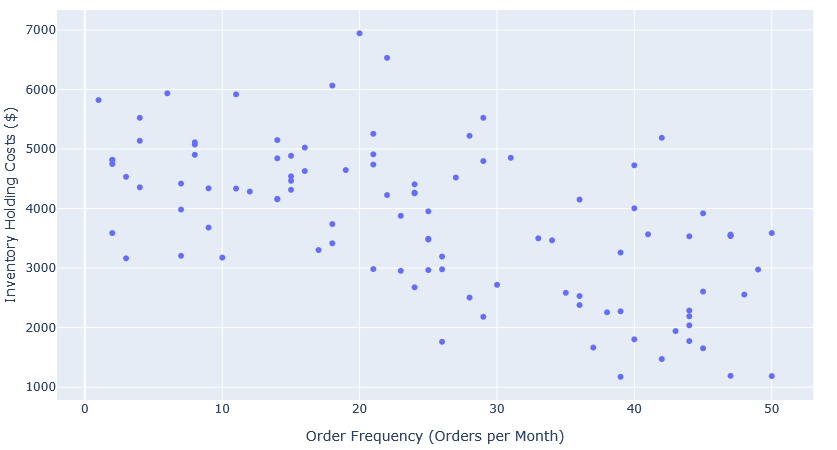
The scatter plot above provides a clear view of how inventory holding costs vary with order frequency. At first glance, we observe that when orders are placed less frequently (fewer than 20 times per month), the inventory holding costs tend to be higher, often exceeding $4,000.
As the order frequency increases beyond 20 orders per month, a general downward trend in holding costs becomes evident. This suggests that more frequent restocking allows the retailer to maintain leaner inventory levels, thereby reducing storage costs. However, this comes with a trade-off: while holding costs decrease, transportation expenses may rise due to more frequent shipments. Interestingly, at very high order frequencies (above 40 orders per month), the variation in holding costs widens. Maybe, there is even an inverse U-shaped relationship? Some products see further cost reductions, while others experience fluctuations. This may indicate diminishing returns - where increasing order frequency beyond a certain point no longer leads to significant cost savings, possibly due to inefficiencies in logistics or supplier constraints.
By applying a regression analysis to this data, retailers can quantify the relationship between order frequency and total costs, helping them identify an optimal ordering strategy that balances storage and transportation expenses effectively. The key takeaway is that more frequent ordering can reduce inventory costs, but only up to a certain threshold before other factors start influencing overall expenses.